Development of a slicing algorithm to compute motion sequences for a rotary 3D-printing system
Bachelor Thesis at group TAMS (also possible as master thesis).Auch in deutscher Sprache möglich.
Motivation
For specific applications, it is useful to 3D-print objects directly on a cylindric "print-bed" instead of the normal flat print-bed that is normally used. For an existing printing system, similar to a normal FFF printer but with a rotating print-bed, we are looking for a person to implement the generation of control sequences (GCode) from a givel geometry model. Existing slicing software solutions cannot directly be applied, as they are not aware of the angle of a rotary axis and do not adapt speed and material volume with increasing circumference of the printed object.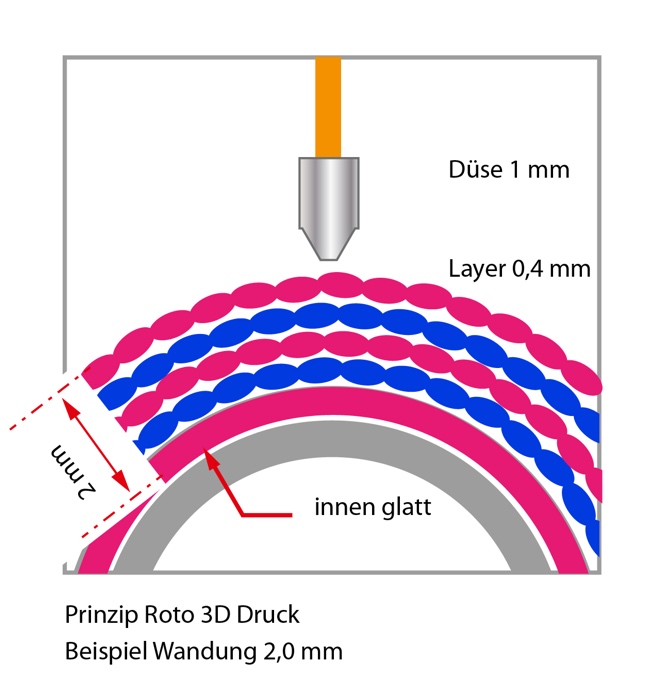 The phyical printing system already exists and is technically capable to print rotary objects.
The phyical printing system already exists and is technically capable to print rotary objects.For the application in this project, the toolpath is computed generatively from a geometric description of the object surface instead of a volumetric CAD-model. Based on a partly existing implementation of a geometry-to-toolpath generator, a toolpath generator should be implemented. The program should compute the rotary transformations, motion sequence, feedrates and extrusion volumes as GCode to be executed on real hardware. In a second step, the rotary axis should be oriented with a given (constant) inclination, to allow overprinting of the entire upper end of the cylinder, as illustrated below.
The existing implementation is done in a visual programming environment (grashopper for Rhino). It is expected that some parts of the solution will be implemented as C# modules, utilizing the OpenNurbs geometry library.
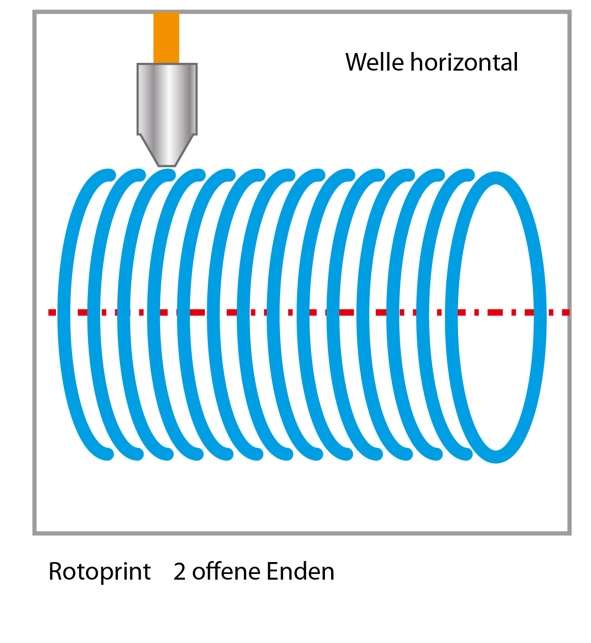
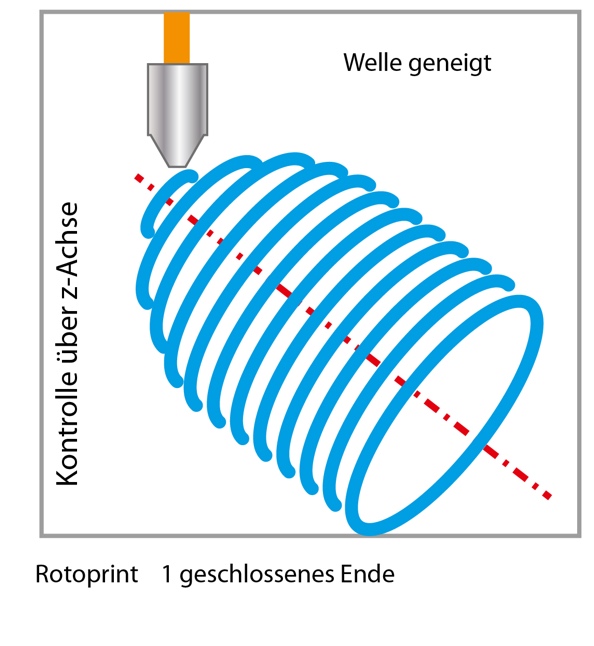
Goals:
- Development of a slicing software to generate GCode with cartesian and angular coordinates
- Calculation of trajectories with velocities and material volumes
- Visualization and error handling
- Evaluation on physical printing system
- Documentation
Requirements
- C++ / C# / Python
- Interest in geometric computing and sequence planning
- (Basic) experience with CAD and 3D-printing
Contact
- Florens Wasserfall, Room F-322, Tel.: +49 (0) 176 57945363
Contact: Dipl.-Ing. Tobias Hackbeil, info@cox3d.de.
COX3D offers a paid working student contract for the duration of the thesis.
Ideal timeframe is first half of 2023.

