Auch die Boolesche Algebra wird wie die lineare Algebra axiomatisch begründet:
Definition: Eine algebraische Struktur {B;∩,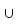 } auf einer wenigstens
zweielementigen Menge B mit den Elementen a, b, c
} auf einer wenigstens
zweielementigen Menge B mit den Elementen a, b, c 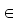 B und den inneren
Verknüpfungen
B und den inneren
Verknüpfungen 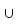 und ∩ heißt ein Boolescher Verband , wenn folgende
Axiome gelten:
und ∩ heißt ein Boolescher Verband , wenn folgende
Axiome gelten:
(B1a) a∩b = b∩a Kommutativgesetz für ∩ (B1b) ab = b
a Kommutativgesetz für
(B2a) (a∩b)
c = (a
c)∩(b
c) Distributivgesetz (B2b) (a
b)∩c = (a∩c)
(b∩c) Distributivgesetz (B3a)
a
B
I
B , so dass a∩I = a Existenz des Einselements (B3b)
a
B
O
B , so dass a
O = a Existenz des Nullelements (B4)
a
B
a'
B, so dass a∩a'= O , a
a' = I Existenz des Komplements
Aus obigen Axiomen lassen sich eine Reihe von Gesetzen ableiten:
(B5a) Es gibt genau ein Nullelement (B5b) Es gibt genau ein Einselement (B6) Zu jedem aB gibt es genau ein Komplement a'
B (B7) (a')' = a (B8a) I' = O (B8b) O' = I (B9) a = b genau dann, wenn a' = b' (B10a) a∩O = O (B10b) a
I = I (B11a) a∩a = a (B11b) a
a = a (B12a) (a∩b)∩c = a∩(b∩c) Assoziativgesetz für ∩ (B12b) (a
b)
c = a
(b
c) Assoziativgesetz für
(B13a) (a∩b)' = a'
b' Theorem von de Morgan (B13b) (a
b)' = a'∩b' Theorem von de Morgan (B14a) a
(a∩b) = a Verschmelzungsgesetz (B14b) a∩(a
b) = a Verschmelzungsgesetz (B15a) a
(a'∩b) = a
b (B15b) a∩(a'
b) = a∩b
Wir werden fortan nur den Booleschen Verband mit den zwei Elementen O = 0 und I = 1 betrachten. Für die Inversion a' von a benutzen wir als Postfixsymbol den Apostroph, weil das satztechnisch einfach ist. Häufig wird statt dessen der Oberstrich verwendet, seltener das Präfixsymbol ¬ . Die Syntax in Programmiersprachen ist wiederum anders. In MATLAB werden folgende Symbole benutzt:
Boolesches Symbol: ∩ (Infix)(Infix) ' (Postfix) MATLAB-Symbol: & (Infix) | (Infix) ~ (Präfix)
Zusätzlich gibt es meistens Funktionen mit üblicher Präfixschreibweise, in MATLAB z.B. die Funktionen and , or und not . So kann man alternativ notieren:
a = 0
b = 1
c = 0
x1 = a | (b & (~c)) % Infixnotation
x2 = or( a , and( b , not(c) ) ) % Präfixnotation
x3 = or( a , b & not(c) ) % Kombination
Üblicherweise gelten die Präzedenzregeln NICHT vor UND vor ODER , so dass man
den Ausdruck für x1 ohne Klammern schreiben kann: x1 = a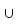 b∩c' . In einigen
MATLAB-Versionen bekommt man aber eine Warnung:
b∩c' . In einigen
MATLAB-Versionen bekommt man aber eine Warnung:
x1 = a | b & ~c % Infixnotation
Die MATLAB-Funktion binexp2bintab berechnet einen als Textstring in MATLAB-Syntax vorliegenden Ausdruck für sämtliche möglichen Kombinationen der binären Variablen:
hilfe( 'binexp2bintab' )
Ein Beispiel ist
binexp2bintab('(a|b) & (~1|c) & (0|c)', {'a'; 'b'; 'c'})
Möchte man die Identität mit einem anderen Ausdruck überprüfen ohne formale Umformung unter Benutzung der Gesetze des Booleschen Verbandes oder möchte man eine solche Umformug verifizieren, so geht das auch mit binexp2bintab :
tabelle1 = binexp2bintab('(a|b) & (~1|c) & (0|c)', {'a'; 'b'; 'c'})
tabelle2 = binexp2bintab('(a|b) & c', {'a'; 'b'; 'c'})
identisch = all(tabelle1==tabelle2) % Überprüfung der Gleichheit
Dies ist zusammengefasst in der Funktion compareexpression(expr1,expr2,vars)
compareexpression( '(a|b) & (~1|c) & (0|c)', '(a|b) & c', {'a'; 'b'; 'c'} )
Auf diese Weise lassen sich z.B. alle aus dem Booleschen Verband hergeleiteten Gesetze überprüfen. Für das erste Assoziativgesetz sieht es wie folgt aus:
compareexpression( '(a&b)&c', 'a&(b&c)', {'a'; 'b'; 'c'} )
Und für deMorgans Gesetz:
compareexpression( '~(a&b)' , '~a|~b' , {'a';'b'} )
Andererseits sind UND und ODER nicht äquivalent:
compareexpression('a&b','a|b',{'a';'b'})