Verknüpfungen in endlichen Mengen lassen sich durch Tabellen definieren. Im Falle der Menge {0,1} hat die Tabelle die Form
| x | |
|---|---|
| + | 0 1 |
| y 0 | a b |
| 1 | c d |
Hierin kommen die vier Konstanten a, b, c, d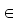 
{0,1} vor. Lässt man
sämtliche Kombinationen der a, b, c, d zu, so ergeben sich 16 verschiedene
innere Verknüpfungen, von denen sich allerdings einige als trivial oder unecht
erweisen. Wir listen zunächst alle auf:
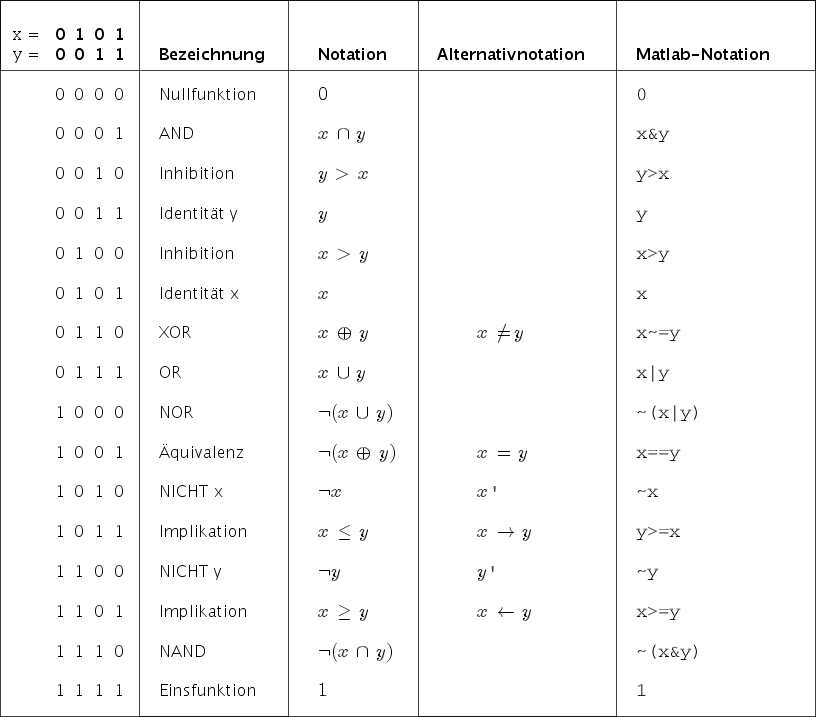
Trivial sind die NULLfunktion und die EINSfunktion, die gar nicht von den zu verknüpfenden Elementen abhängen, und unecht sind alle Funktionen, die nur von einem der beiden Elemente abhängen. Das sind NICHTx, NICHTy, Identität x und Identität y. Es verbleiben folgende echte Verknüpfungen, für die wir die Gültigkeit der Gruppenaxiome mit auflisten:
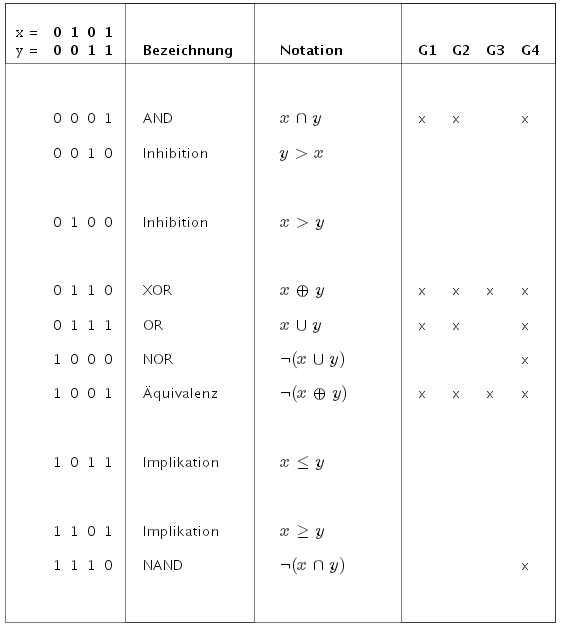
Eine Algebra, in der Gleichungssysteme lösbar sein sollen, benötigt eine innere Verknüpfung mit inversen Elementen. Nur das XOR und die Äquivalenz bieten dies. Die Codierungstheorie arbeitet deshalb mit der GF(2)-Algebra.
Für die Realisierung von beliebigen Funktionen ist es wichtig zu wissen, welche dieser Verknüpfungen unverzichtbar sind oder mit welchen Untermengen man sämtliche Funktionen realisieren kann.
Definition: Eine Menge M von inneren Verknüpfungen von A und einstelligen Operationen heißt funktional vollständig , wenn mit ihnen alle Funktionen f : An → A geschrieben werden können.
Beispiele von funktional vollständigen Mengen für B = {0,1} ---------------------------------------------------------------------------------
M = {NAND} übliche Computer-Logik
M = {NOR} früher zum Teil bei ECL-Logik verwendet
M = {UND, NICHT}
M = {ODER, NICHT}
M = {XOR, UND, EINS} endlicher Körper GF(2)
M = {UND, ODER, NICHT} Boolesche Algebra
Die übliche Computerlogik arbeitet also mit einer schwer handhabbaren Algebra, in der nur G4 gilt. Zur Entscheidungsfindung innerhalb von Rechenprogrammen und auch beim Entwurf von Hardware wird dagegen die Boolesche Algebra verwendet, in der es keine einheitlichen Inversen Elemente gibt, so dass keine eleganten Verfahren zur Lösung von Gleichungssystemen möglich sind. Der folgende Abschnitt beschäftigt sich mit der Booleschen Algebra. Die Funktionale Vollständigkeit der Booleschen Algebra wird im Kapitel 7 gezeigt. Die Funktionale Vollständigkeit der übrigen Mengen lässt sich daraus ableiten durch Realisierung von UND, ODER und NICHT durch die jeweilige Verknüpfungsmenge.