Multiplexer sind Datenselektoren: Es gibt k Bündel von je n Bit als Dateneingänge, von denen jeweils einer auf den n-Bit-breiten Ausgang durchgeschaltet wird. Die Auswahl erfolgt durch eine m-Bit-breite Steuergrösse s . Zumeist ist k eine Potenz von 2 und m = log2(k) . Man spricht dann von einem n-fach-k-zu-1-Multiplexer.
Das folgende Bild stellt eine Schema des Multiplexers dar:
drawmux(2)
Der Multiplexer ist eines der wichtigsten Bausteine auf der R-T-Ebene.
Der 2-zu-1-Multiplexer ist funktional vollständig.
Das Verhalten des n-fach-k-zu-1-Multiplexers ist in allen Programmiersprachen
mit speziellen Sprachkonstrukten beschreibbar, ein 4-zu-1-Multiplexer mit den Eingängen
a, b, c, d und der Steuergrösse s (s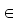
{0,1,2,3} in MATLAB z.B. durch
switch s case 0, y = a; case 1, y = b; case 2, y = c; case 3, y = d; end
Multiplexer lassen sich mit relativ geringem Aufwand realisieren.
Der 2-zu-1-Multiplexer für ein Bit wurde schon als Schaltfunktion besprochen:
y = ~s∩a 
s∩b
Für eine Breite von n Bit der Eingänge wird dieses n mal parallel realisiert. Den 4-zu-1-Multiplexer realisiert man entweder direkt in der Form
y = s1'∩s2'∩a
oder unter rekursiver Verwendung von 2-zu-1-Multiplexern mux(s,a,b) :
y = mux( s2, mux(s1,a,b), mux(s1,c,d) )
Übung: Geben Sie den Realisierungsaufwand M1, M2, Z1, Z2 für beide Strukturen in Abhängigkeit der Bitbreite k und der Anzahl der Eingänge n = 2m an.
Die rekursive Methode ist besonders aufwandsarm, aber langsamer.