8.3.1 Modelle

Bei der Betrachtung von Schaltfunktionen kommt der Begriff der Zeit nicht vor. Die technische Repräsentation einer Schaltfunktion soll jedoch im zeitlichen Nacheinander für verschiedene Argumente den Funktionswert liefern. Anstelle einer Schaltfunktion 

        f : Bn  →  B

müssen wir also betrachten: 

        f : Sn  →  S  , wo    S = { s | s : T  →  B}

Hier steht T für die reelle Zeit.

Das Zeitverhalten ist stark von der physikalischen Realisierung abhängig und überdies selbst bei festgelegter Realisierung nicht genau vorhersagbar.
Dennoch wollen wir das Zeitverhalten von logischen Verknüpfungen und Schaltnetzen so weit wie möglich schon auf der in diesem Kapitel relevanten Abstraktionsebene modellieren. Dazu definieren wir zunächst die zeitliche Verzögerung:

Def. Sei S = { s | s : T → B} , wo T für die reelle Zeit steht. Dann heißt g : S → S Verzögerung (delay) um die Zeit τ , wenn für alle x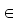S und y = g(x) gilt: y(t + τ) = x(t) .

Das folgende Bild stellt als Beispiel ein Signal und eine Verzögerung des Signals dar: 

delaygraph

Bei gedrückter Maus wird der Mauszeiger zu einem Fadenkreuz.

Ein Modell soll sein:

(1) so einfach wie möglich
(2) so detailliert wie nötig

Wir betrachten zwei Modelle des Zeitverhaltens von Schaltfunktionen:

1. Das fundamentale Modell

In diesem Modell wird nur eine Verzögerung am Ausgang der Schaltfunktion f angenommen: y(t+τ) = f(x(t)) .
Dieses Modell ist dann ausreichend, wenn das Ausgabesignal des Schaltnetzes im Zeitintervall von der letzten Änderung der Eingabe bis zum Ablauf der nachfolgenden Verzögerung irrelevant ist.

2. Das Gattermodell

Für jede Verknüpfung innerhalb der Realisierung der Schaltfunktion wird eine individuelle Verzögerung angenommen.

Auch im Fall des Gattermodells kann man das logische Verhalten vom Zeitverhalten trennen. Dazu muss man das Verzögerungsverhalten aller logischen Verknüpfungen in ein verzögertes Ablesen der Inputvariablen transformieren: 

 y(t+τ) = g(x1(t),x2(t))  =>  y(t) = g(x1(t-τ),x2(t-τ))

Auf diese Weise gelingt es, Schaltnetze weiterhin als verzögerungsfreie Bündel mathematischer Funktionen zu modellieren, deren Inputvariable jedoch individuell zeitversetzte Signale sind. Dabei hat jedes Vorkommen der selben Variablen im schaltalgebraischen Ausdruck eine individuelle Verzögerung.
Sei z.B. in der Schaltfunktion 

 a'  (a∩b')  b

die Verzögerung der UND-Verknüpfung τ1 und die der ODER-Verknüpfung τ2 , so ergibt sich 

 y(t) = a(t-τ2)'  (a(t-τ1-τ2)∩b(t-τ1-τ2)')  b(t-τ2)

Tatsächlich ist die hier gewählte Schaltfunktion identisch mit der konstanten Eins, also völlig unabhängig von den Argumenten a und b . Dennoch kann man natürlich diese nicht minimale Form des Ausdrucks realisieren. Wir werden weiter unten und speziell im folgenden Abschnitt sehen, dass das Zeitverhalten verschiedener Realisierungen der selben zugrundeliegenden Schaltfunktion verschieden ist. Deshalb kann auch die Ausgabe einer Realisierung der konstanten Funktion durchaus von der Konstanten abweichen.

Die Ausdrücke sind deutlich übersichtlicher und vor allem leichter automatisch zu behandeln bei systematischer Klammerung ohne Präzedenzregeln und ausschließlicher Benutzung der Präfix-Notation. Anstelle der Infixsymbole ∩ & * wird nachfolgend häufig die Funktion all benutzt, die als Parameter einen Vektor hat (mit eckigen Klammern), in dem sämtliche Eingabevariablen verzeichnet sind. Die entsprechende Funktion für das ODER ( 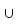| ) ist any . 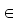Diese Schreibweise mit einem Vektor als Variable ist auch mathematisch präziser, denn die Schaltfunktionen sind ja definiert als f : Bn → B , Argument der Funktion ist also ein Vektor Bn . Die im vorigen Beispiel benutzte Funktion notiert sich damit wie folgt: 

binexpr2prefix('~a&(b|c)')

Die Funktionstabelle ist 

binexp2bintab( '~a&(b|c)' , {'a';'b';'c'} , 2 )

Wir weisen nun den Verknüpfungen in der Reihenfolge ihres Auftretens in dem Baum-artigen Ausdruck Verzögerungen zu. Diese sind als Vektor von natürlichen Zahlen als zweite Parameter der Funktion drawdelay anzugeben. Wir betrachten das Zeitverhalten für das spezielle Inputsignal, das die Bitmuster der Funktionstabelle der Reihe nach von oben nach unten für jeweils 10 Zeiteinheiten anlegt: 

drawdelay('~a&(b|c)' , [1 1] )

Offenbar entspricht das Ausgabesignal nicht genau der Funktionstabelle. Wir werden dieses Problem im folgenden Abschnitt über Hasards behandeln.

Im Falle des fundamentalen Modells wird nur eine pauschale Verzögerung angenommen. Wir modellieren diese als Verzögerung der Wurzel des Ausdrucks und setzen alle anderen Verzögerungen auf Null: 

drawdelay( '~a&(b|c)' , [2 0] );  % Zeitdiagramm

Bei Benutzung des fundamentalen Modells tritt der Hasard nicht in Erscheinung. Außerdem ist hier die fallende Flanke des Ausgabesignals stärker verzögert als im Falle des Gattermodells.

Das Gattermodell ist zwar deutlich komplizierter, löst dafür aber Feinheiten des zeitlichen Verhaltens auf.

Wir kommen noch einmal auf die oben besprochene umständliche Realisierung einer konstanten Eins im Gattermodell zurück: 

drawdelay( '~a|(a&a)' , [1 1] );  % Zeitdiagramm

Diese Realisierung wandelt jede steigende Flanke des Inputsignals in einen inversen Impuls.