6.2 Gruppe

Eine sehr einfache algebraische Struktur ist die Gruppe:

Definition: Eine nichtleere Menge G mit einer inneren Verknüpfung ο heißt eine Gruppe , wenn die folgenden Axiome erfüllt sind:

G1 Assoziativgesetz : 

 (a ο b) ο c = a ο (b ο c)     a,b,c  G

G2 Existenz eines neutralen Elements :

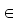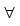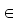Es gibt genau ein e G , so dass e ο a = a ο e = a a G

G3 Existenz der inversen Elemente :

Zu jedem a 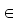G gibt es genau ein a-1 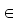G mit a-1 ο a = a ο a-1 = e

Beispiel:

In der Menge {A,B,C} sei eine innere Verknüpfung definiert durch folgende Tabelle:

x
ο A B C
A C A B
y B A B C
C B C A

Dem Leser sei als Übungsaufgabe die Überprüfung von G1, G2 und G3 überlassen. Die hier definierte innere Verknüpfung erfüllt überdies das

G4 Kommutativgesetz : 

 a ο b = b ο a     a,b   G

Wenn in einer Gruppe das Kommutativgesetz gilt, liegt eine kommutative Gruppe vor. Sie wird auch als Abelsche Gruppe bezeichnet.

Die einfachste Gruppe ist die triviale Gruppe aus einem einzigen Element, das mit sich selbst verknüpft wieder sich selbst ergibt. Der Nachweis von G1 bis G4 ist trivial.

Die für die technische Informatik wichtigste Gruppe ist ({0,1},+) :

x
+ 0 1
y 0 0 1
1 1 0

Die hier mit dem Infixsymbol + definierte innere Verknüpfung wird auch als exklusives Oder bezeichnet.

Bei kleinen endlichen Mengen kann man den Nachweis der Gruppenaxiome dem Rechner überlassen, der sturheil sämtliche Kombinationen durchprobiert: 

isgru([1 2; 2 1])

Parameter von isgru ist die Tabelle der inneren Verknüpfung in Indexform, d.h. die Elemente der Menge sind in beliebiger Reihenfolge durchnummeriert von 1 bis n . Prüfen Sie mit isgru durch entsprechende Umsetzung auch die Gruppenaxiome für die oben als Beipiel angegebene Verknüpfungstabelle der Menge {A,B,C} und prüfen Sie ebenfalls die triviale Menge.

Die dümmste Methode der Konstruktion von endlichen Gruppen ist die Generierung der Verknüpfungstabelle durch Zufallszahlen. Die benötigte Rechenzeit steigt exponentiell mit der Gruppengröße n : 

n = 3;
for k=1:10000 
   tab = ceil(n*rand(n,n)); 
   b   = isgru(tab); 
   if b break; end; 
end; 
if b
  Verknuepfungstabelle = tab;
  result2fig(Verknuepfungstabelle)
  isgru(tab); 
end