Information
Ai seien sich gegenseitig ausschließende Ereignisse, die zufällig eintreffen. Als stochastisches Modell, welches die Zufälligkeit näher beschreibt, gelte
W{Ai} = pi
Dies sei die Schreibweise für "das Ereignis Ai tritt mit der Wahrscheinlichkeit pi ein. Bei der Übertragung von Informationen sagen wir anstelle von "das Ergebnis Ai tritt ein" "wir empfangen das Symbol Ai". Inhaltlich ist das natürlich dasselbe.
Angenommen es ist pi = 1 und pj = 0 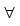 j ≠ i , und dem Empfänger sei dies
bekannt. Dann empfangen wir mit Sicherheit (pi = 1) das Symbol Ai . Es gibt also
keine Überraschung. Dass Ai ankommt, ist für den Empfänger "nichts Neues". Der
Empfang bringt also keinen Informationsgewinn. Der Informationsgehalt der Sendung
eines Symbols, dessen Wahrscheinlichkeit 1 ist, ist 0 .
j ≠ i , und dem Empfänger sei dies
bekannt. Dann empfangen wir mit Sicherheit (pi = 1) das Symbol Ai . Es gibt also
keine Überraschung. Dass Ai ankommt, ist für den Empfänger "nichts Neues". Der
Empfang bringt also keinen Informationsgewinn. Der Informationsgehalt der Sendung
eines Symbols, dessen Wahrscheinlichkeit 1 ist, ist 0 .
Sind die pi dagegen sehr verschieden und pi ≠ 1 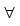 i , so ist die
Überraschung größer bei Empfang von Ai mit kleinem pi . Setzt man das Maß
für den Informationsgehalt mit "Überraschung" gleich, so wäre dafür eine mögliche
Quantifizierung 1/pi . Ein einfaches Beispiel zeigt jedoch, dass dieses nicht
geeignet ist:
i , so ist die
Überraschung größer bei Empfang von Ai mit kleinem pi . Setzt man das Maß
für den Informationsgehalt mit "Überraschung" gleich, so wäre dafür eine mögliche
Quantifizierung 1/pi . Ein einfaches Beispiel zeigt jedoch, dass dieses nicht
geeignet ist:
Man erhalte die Information A , deren Wahrscheinlichkeit pA ist, und danach noch die davon unabhängige Information B , deren Wahrscheinlichkeit pB ist. Wegen der Unabhängigkeit ist die Wahrscheinlichkeit beider Ergeignisse gegeben durch das Produkt pA*pB . Also würde mit 1/p als Maß für den Informationsgehalt gelten: Der Informationsgehalt zweier Ereignisse ist das Produkt der Informationsgehalte beider Ereignisse. Das widerspricht aber der Vorstellung einer Größe, die einen Gehalt messen soll und damit additiv sein muss. Diese Additivität ist leicht herzustellen, nämlich durch Logarithmierung:
Wir definieren als Informationsgehalt eines Ereignisses Ai der Wahrscheinlichkeit pi
I(Ai) = log2(1/pi) = -log2(pi)
Neben den Bezeichnungen "Information" und "Informationsgehalt" ist für diese Größe auch "Entscheidungsgehalt" geläufig.
Für den oben durchgespielten Fall von zwei Ereignissen A und B hat man dann
I(A) + I(B) = log2(1/(pA*pB)) = log2(1/pA) + log2(1/pB) = I(A) + I(B)
in Übereinstimmung mit der Forderung nach einer additiven Größe.
log2 bedeutet der Logarithmus zur Basis 2 . Die Einheit der so definierten Information ist 1 Bit. Dies sollte nicht verwechselt werden mit Binärstellen oder den Symbolen 0 und 1. Als Logarithmus ist der Informationsgehalt eine reelle Größe. Dass diese Begriffsbestimmung dennoch sehr sinnvoll ist, zeigt der Empang einer Binärstelle: Möglich seien nur die beiden Empfangssymbole "0" und "1" , und zwar beide mit gleicher Wahrscheinlichkeit p0 = p1 = 1/2 . Der Informationsgehalt des Empfangs einer "0" oder einer "1" ist dann
I("0") = I("1") = log2(1/(1/2)) = 1 Bit
Die Begriffe "Ungewissheit", "Überraschung" und "Information" hängen auf folgende Weise zusammen:
Vor dem Empfang gibt es die Ungewissheit über das Kommende.
Beim Empfang gibt es die Überraschung.
Und danach hat man den Gewinn an Information.
Alle drei Begriffe wollen wir mit demselben oben definierten Betrag messen.
Diese Quantifizierung des Begriffes "Information" ist zugeschnitten auf die
speziellen Belange der Nachrichtentechnik. Sie kann nicht allen Aspekten des
umgangssprachlichen Globalbegriffes gerecht werden.
Beispiel 1 :
Die Wahrscheinlichkeit, an einem bestimmten Tag von einem Meteor erschlagen zu
werden, sei
p = 10^-16 % p = 0.0000000000000001
Dieses doppelklicken, damit p den gewünschten Wert bekommt.
Man sieht diesem Tag zuversichtlich entgegen, weil die Ungewissheit von
log2(1/(1 - p)) % 0.00000000000000033307
außerordentlich klein ist. Ebenso klein ist die Überraschung, wenn das Unglück nicht passiert. Und der Informationswert der Nachricht "Ich wurde nicht vom Meteor erschlagen" ist ebenso gering. Umgekehrt wäre die Überraschung groß, nämlich
log2(1/p) % 53.1508
wenn das Unglück tatsächlich geschähe. Und wegen des hohen Informationsmaßes von 53 würden alle Medien die Nachricht auch dann bringen, wenn es nicht eine bekannte Persönlichkeit getroffen hat.
Beispiel 2 :
Die "6" beim Würfeln hat bei vielen Spielern eine besondere Bedeutung. Bedeutung
oder gar Konsequenz von Symbolen wird hier nicht betrachtet, sondern nur ihre
Wahrscheinlichkeit, und die ist für die "6" die selbe wie für alle anderen Seiten
des Würfels.
Beispiel 3 :
Gegeben seien zwei Bücher von je 200 Seiten zu je 40 Zeilen von je 72 Zeichen.
(a) deutscher Text
(b) alle Typen mit Zufallsgenerator mit Gleichverteilung eines Alphabets von
80 Zeichen erzeugt
Welches enthält die meiste Information?
Empfangen wir im deutschen Text "Der Begrif", so ist f als nächstes Symbol kaum
eine Überraschung, während der Zufallstext mit jedem Symbol die zusätzliche
Information log2(1/(1/80)) liefert. Der Zufallstext
enthält also die größtmögliche Information.
Das Beispiel offenbart noch einen wichtigen Punkt:
Kennt der Empfänger den Algorithmus des Zufallsgenerators, so gibt es gar keine
Überraschung mehr. In diesem Fall wird jedes Symbol mit der Gewißheit p = 1
empfangen, und der Informationsgehalt ist 0 .
Beispiel 4 :
Die Wahrscheinlichkeit, in einem Text an einer gegebenen Stelle das Zeichen "A"
anzutreffen, sei W{A} = p = 0.01 . Dann ist der Informationsgehalt des Zeichens
log2(1/0.01) % 6.6439
Wenn der Text als ASCII-Text vorliegt, werden 8 Binärstellen zur Repräsentation des "A" benutzt. Der Informationsgehalt ist jedoch geringer.
Entropie
Die Definition der Information läßt sich nur jeweils auf den Empfang eines speziellen Zeichens anwenden. Wir fragen deshalb jetzt global nach der durchschnittlichen Information, die der Empfang eines Symbols liefert. Diesen Erwartungswert bezeichnet man als Entropie des Systems.
Die Wahrscheinlichkeiten aller möglichen Ereignisse Ai seien W{Ai} = pi . Da jeweils ein Symbol aus der Menge aller möglichen eintritt, ist die Summe aller pi gleich 1 .
Dann ist die Entropie ( E steht für Erwartungswert)
n n n
H = E{I(Ai)} = Σ pi I(Ai) = Σ pi log2(1/pi) = - Σ pi log2(pi)
i=1 i=1 i=1
Die Entropie ist nur eine Funktion der Wahrscheinlichkeiten pi , also nur abhängig vom stochastischen Modell.
Beispiel 1
Es gebe 3 mögliche Ereignisse mit den Wahrscheinlichketen 1/2 , 1/3 , 1/6 :
Die Entropie ergibt sich zu
p = [ 1/2 1/3 1/6 ] H = sum( p .* log2( 1./p )) % H = 1.4591
Die Punkte vor den Operationssymbolen * und / bedeuten in der MATLAB-Syntax, dass diese Operationen bei Vektoren und Matrizen elementweise auszuführen sind.
Der einfache Ausdruck für H ist in der Funktion entropie(p) realisiert:
entropie( [ 1/2 1/3 1/6 ] )
Beispiel 2
Empfang einer Binärstelle mit den Wahrscheinlickeiten p0 = q ; p1 = 1 - q Im Fall q = 1/2 erhält man:
entropie( [ 1/2 1-1/2 ] )
Der mittlere Informationsgehalt beim Empfang einer Binärstelle mit gleicher Wahrscheinlichkeit für beide Symbole ist also genau 1 Bit.
Die Abhängigkeit von q wird in folgendem Bild dargestellt:
plotentropy
Der mittlere Informationsgehalt einer Binärstelle ist offenbar nur dann 1 Bit, wenn beide möglichen Symbole gleich wahrscheinlich sind. Entsprechendes gilt auch für größere Symbolmengen. Sind z.B. alle 256 8-Bit-Bytes gleich wahrscheinlich, so ist die Entropie wie erwartet 8 Bit :
H = 256 * 1/256 * log2( 1/(1/256) )
Berechnet: ( ones(m,n) liefert eine m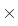 n-Matrix von Einsen )
n-Matrix von Einsen )
entropie( ones(1,256)/256 )
Redundanz
Als Redundanz wird die Differenz zwischen dem aufgrund der Wortlängen möglichen und dem tatsächlich genutzten mittleren Informationsgehalt bezeichnet.
Kanalkapazität
Die Informationstheorie wurde entwickelt als Theorie zur formalen Behandlung der Übertragung von Information über reale nicht fehlerfreie Kanäle, deren Fehlerverhalten sich aber in einem stochastischen Modell formulieren lässt. Für den wichtigen binären symmetrischen Kanal geben wir hier ohne längliche Herleitung die sog. Kanalkapazität C an, d.h. den maximal pro Binärstelle übertragbaren Informationsgehalt:
C = 1 - H(F)
Hierin ist H(F) die Entropie des Fehlerverhaltens.
Der binäre symmetrische Kanal sei festgelegt durch folgende Eigenschaften:
(1) Die Wahrscheinlichkeit der beiden Symbole 0 und 1 ist gleich.
(2) Die Wahrscheinlichkeit P , dass aus einer 0 eine 1 wird, ist gleich
der Wahrscheinlichkeit, dass aus einer 1 eine 0 wird.
(3) Die Wahrscheinlichkeit eines Fehlers an der Binärstelle i ist
unabhängig vom Auftreten der Fehler an anderen Stellen.
Damit ist H(F) = P*log2(1/P) + (1 - P)*log2(1/(1-P)) .
Die Kanalkapazität des binären symmetrischen Kanals in Abhängigkeit der Fehlerwahrscheinlichkeit P zeigt das folgende Bild:
plotcapacity
Offenbar ist die Kanalkapazität 0 bei P = 0.5 . Der Empfänger kann in diesem Fall die empfangene Bitsequenz nicht von einer zufälligen Bitsequenz unterscheiden. Dass die Kanalkapazität bei P > 0.5 wieder ansteigt, liegt daran, dass man in diesem akademischen Fall durch Inversion aller Bits eine Sequenz erzeugt, für die die Bitfehlerwahrscheinlichkeit 1 - P ist.
Die Kanalkapazität ist eine obere Schranke, die in der Praxis nicht erreicht wird. Die formale Herleitung gibt auch keinerlei Hinweise, wie überhaupt eine praktisch fehlerfreie Übertragung möglich werden könnte. Wir versuchen dies im folgenden Abschnitt.