Wissenschaft hat man auf allen Gebieten betrieben, bevor die Gebiete sich im einzelnen herauskristallisiert haben und einen eigenen Namen bekamen.
Die Definition der Informatik aus dem vorigen Kapitel setzt den programmierbaren Rechner nicht voraus. Überall, wo gemessen und Gemessenes verwaltet wurde, war Informatik.
Die Länge des Jahres von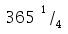 
Tagen war immerhin bekannt vor 6230 Jahren.
Für solch eine Messung muss es nicht nur Messverfahren geben, sondern auch
Möglichkeiten der sprachlichen Bezeichnung und der schriftlichen Fixierung von
Zahlen der Größenordnung 10000 .
Beispiele für alte Schriften von Zahlen geben die folgenden Bilder. Lange vor der Erfindung der Schrift wurden Zählsymbole benutzt:
openbyextension('susa-tonkugel.jpg')
Die etwa 5000 Jahre alten versiegelten Tonkugeln enthielten stellvertretend für irgendetwas die Zählsymbole. Auf diese Weise konnte man vor der Einführung der Schrift quantitativ festgelegte Verträge abschließen.
Nippur in Mesopotamien, wo man ca. 50000 Tontafeln fand, wurde im Jahre -1955 von den Elamiten zerstört. Die Tafeln sind also durchweg älter. Dies ist etwa die Zeit, als die Abstraktion zur Zahl an sich vollzogen wurde. Sehr lange vorher hat man schon genau Buch geführt, jedoch bei Zahlenangaben grundsätzlich das Gezählte mit benannt. Die meisten Zahlennotationen galten sogar jeweils nur für Getreide bzw. für Grundstückgrößen, für Stück Vieh usw..
Bierzuteilungen an bestimmte Personen für bestimmte Veranstaltungen:
openbyextension('bierzuteilungen.jpg')
Wie heute wurden Dokumente auch damals kopiert und an mehreren Stellen verwahrt:
openbyextension('uebersetzung.jpg')
Viel jünger, nämlich 3400 Jahre alt Wandmalereien aus Abd-el-Qurna, die sehr schön das Messen und Registrieren zeigen.
openbyextension('abd-el-qurna.jpg')
Das Messen ist der Ursprung der Zahl. Die Zahl ist die Abstraktion vom Gemessenen und beruht auf dem Distributivgesetz für Anzahlen von Dingen, die man abzählen kann:
distributivzahl
Es gilt also
a X + b X = (a + b) X
wo a und b und a + b Anzahlen der zu zählenden Einheit X sind. X steht z.B. für Äpfel, Euro etc.
Weitere Beispiele:
Eine Schulübung zur Notation der Zahlen 1 bis 9 aus Mesopotamien:
openbyextension('schuluebung.jpg')
Diese folgende Tafel aus Schuruppak hat 104 Eintragungen über die Grösse von Feldern und die Namen und Berufe der Eigentümer. Die Tafel stammt aus der Zeit um 2600 v.Chr:
openbyextension('schuruppak.jpg')
Eine Jahresabrechnung über die Tätigkeit von 36 Arbeiterinnen zum Mahlen von Mehl mit der Gesamtgenauigkeit von 1/6 Arbeitstag bzw. ca. ½ Liter Mehl:
openbyextension('jahresabrechnung.jpg')
Ägyptische Hieroglyphen mit Zahlenangaben:
openbyextension('aegyptisch.jpg')
Die alten Zahlenschriften sind nicht gut geeignet für Algorithmen zur Addition und Multiplikation. Z.B. wäre die Addition einer Mehrwertsteuer von 16% sehr kompliziert. Dieses Problem wurde damals durch Tabellen gelöst, die ein erstes Beispiel für Datenstrukturen liefern.
Auch kannte man das Problem von Diskrepanzen zwischen karteimäßig geführten und tatsächlich vorhandenen Beständen und fand Lagermethoden, die einerseits das Entwenden erschwerten und andererseits auch die Ermittlung von Diskrepanzen ermöglichten. Das folgende Bild aus Kalkutta gibt ein Beispiel.
openbyextension('kalkutta.jpg')
Wieviele Kugeln mag der große Haufen rechts im Vordergrund enthalten ?
ca.: 100 400 1600 6400 ??
Auch in Nippur fand man Tontafeln mit Tabellen der Dreiecks und Pyramidenzahlen. Sei die Breite (und damit auch die Giebelseite) der Pyramide n und die Firstlänge m , dann ist der Pyramideninhalt
n n
(m - 1)Σ i + Σ i2
i=1 i=1
Dies lässt sich umformen in
n*(n+1)*((2*n+1)/3 + m - 1)/2
Diese Funktion pyramidenzahl(n,m) ergibt:
pyramidenzahl(23,8)
Das Sexagesimalsystem der Sumerer - jedoch nicht seine Schreibweise - hat sich bis heute über die Griechen und Römer in der Zeit- und Winkeleinteilung erhalten.
Ein technisches Hilfsmittel für die algorithmische Durchführung arithmetischer Operationen ist der Abacus. Im folgenden Bild ist die Addition mit einem japanischen gezeigt. Der Abacus ist ein Akkumulator. Er ist Stellen-orientiert und kennt die Null. Dies ist den ersten Benutzern wohl nicht bewusst gewesen.
openbyextension('abacus.jpg')
Einen Abacus auf dem OH-Projektor mit einer mehrstelligen Addition vorführen.
Die neuere Geschichte wird durch die nachfolgenden Bilder illustriert:
Der Universahlgelehrte Leibnitz hat nicht nur das Binär-System eingeführt sondern auch Rechenmaschinen erfunden:
openbyextension('leibnitz.jpg')
Der Pfarrer Philip Matthäus Hahn konstruierte erstmals Maschinen mit dem Ziel der leichten Reparierbarkeit und betrieb eine Fabrik:
openbyextension('phmhahn.jpg')
Charles Babbage konstruierte zunächst eine Maschine zur berechnung von Tabellen:
openbyextension('babbagediffeng.jpg')
Dabei entdeckte er die Möglichkeit der allgemeinen Programmierbarkeit eines solchen Automaten. Seine Konstruktion einer solchen programmierbaren Maschine ist wegen technische Probleme nie lauffähig geworden:
openbyextension('babbageanalyteng.jpg')
Konrad Zuse baute den ersten Rechenautomaten mit Binärsystem:
openbyextension('Z1-v3.jpg')
openbyextension('Z1-vb2.jpg')
openbyextension('Z1-ble.jpg')
Die Z3 von Zuse:
openbyextension('Z3.jpg')
Die Havard Mark 1:
openbyextension('mark1.jpg')