Die Gleichung z = z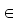 ; z
B = {0,1} hat die zwei Lösungen z = 0 und z = 1 .
Eine physikalische Realisierung dieses Trivialschaltwerks mit znext = z würde also
den beim Einschalten des Schaltwerks angenommenen Zustand bis zum Auschalten
beibehalten. Eine physikalische Realisierung bedarf allerdings einer Energiezufuhr.
Deshalb reicht eine einfache Drahtschleife nicht zur Realisierung von z = z . Die
aufwandärmste Form ist meistens die Hintereinanderschaltung zweier Inverter, also
znext = (z')' .
Das beschriebene Speicherelement kann zwar sowohl die 0 wie auch die 1 speichern, aber ändern kann man den Speicherinhalt nicht. Um dies zu erreichen führt man zwei Inputvariable ein: den Dateninput D und den Takt C . Im Falle eines taktpegelgesteuerten Zeitgliedes gilt dann:
znext = C'∩z 
C∩D
Dies ist ein 2-zu-1-Multiplexer, der mit dem Takt C gesteuert wird und dessen einer Eingang (im Falle C = 0 ) mit dem Ausgang verbunden ist (Speicherfunktion) und dessen anderer Eingang zum Einspeichern eines neuen Datenwerts dient. Das Mealy-Modell des Speichergliedes ist dann:
drawmuxff
Der Folgezustand wird hier direkt auch als Ausgabe verwendet. Im Sinne des Mealy-Modells wäre es korrekter gewesen, das Multiplexer-Schaltnetz zweimal zu zeichnen. Greift man den Ausgang Q nicht bei znext ab sondern bei z , so liegt ein Moore-Modell vor. Da das Zeitglied nur eine Verzögerung darstellt, gibt es bei der Realisierung der beiden Modelle keinen Unterschied.
Das KV-Diagramm ist
kvdiagram('(~C&z) | (C&D)',{'C';'D';'z'},{[2 4] [8 7]},1)
In diesem KV-Diagramm ist ein Strukturhasard offensichtlich. Dass dieser tatsächlich essentiell ist, kann man am Verhalten des Schaltwerks erkennen, wenn man probehalber die Verzögerungen variiert. Wir berechnen zunächst das Verhalten ohne Verzögerungen ausser der notwendigen Verzögerung von 1 in der Rückkopplung:
drawsigsmuxff( [1 0 0] )
Nun wird die Verzögerung der beiden UND-Glieder unterschiedlich gewählt:
drawsigsmuxff( [1 1 0] ) % unterschiedliche Verzögerung der UND-Glieder
Hier wird die Verzögerung der beiden UND-Glieder vertauscht:
drawsigsmuxff( [1 0 1] ) % unterschiedliche Verzögerung der UND-Glieder
Offenbar funktioniert das Speichern einer 1 nicht mehr oder es treten statische 0-Hasards im Zustand und damit auch in der Ausgabe auf.
Der Strukturhasard ist wie im Abschnitt 8.3.2 beschrieben leicht durch eine zusätzliche Schleife im KV-Diagramm zu beseitigen:
kvdiagram('(~C&z) | (C&D) | (D&z)',{'C';'D';'z'},{[2 4] [8 7] [4 8]},3)
Dieses Hasard-freie pegelgesteuerte D-Flipflop heisst Earle-Latch. Das Mealy-Modell bzw. das einfache Schaltbild ist:
drawearlelatch(1) % Mealy-Modell des Earle-Latch
drawearlelatch(0) % Schaltbild des Earle-Latch
Jetzt arbeitet es auch bei beliebigen zufälligen Verzögerungen korrekt:
Mehrfach aufrufen wegen der zufälligen Verzögerungen!
drawsigsearle(ceil(4*rand(1,4)))
Das Schaltnetz des Earle-Latch ist frei von Strukturhasards. Wettläufe kann es nicht geben, da es nur ein einziges Zustandsbit in der Rückkopplung gibt. Dieses nichtgetaktete Schaltwerk arbeitet deshalb sicher auch bei beliebigen individuellen Verzögerungen der Verknüpfungen, solange die generelle Voraussetzung für nichtgetaktete Schaltwerke eingehalten wird, dass nämlich der Input sich nur einschrittig ändert, und auch nur dann, wenn sich das Schaltwerk in einem stabilen Zustand befindet. Wir kommen auf dieses Thema zurück im Abschnitt 10.5 .
Das Zustandsdiagramm des taktpegelgesteuerten Flipflops ist sehr einfach, weil es aufgrund des einzigen Zustandsbit nur zwei Zustände gibt:
demofsm([1 1 2 1; 2 1 2 2],{'0';'1'},1,1,{'00';'01';'11';'10'},'D,C')