TAMS / Java / Hades / applets (print version): contents | previous | nextLFSR linear feedback shift register (8-bit)
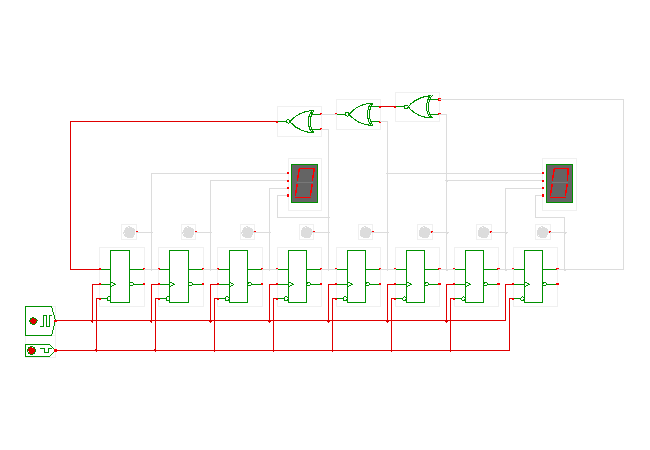 DescriptionA simple 8-bit linear feedback shift register
built from D-flipflops.
In this example, the outputs of flipflops 8,6,5,4 are summed
via XNOR gates (this is a linear operation, hence the name)
and fed back into the first flipflop.
Just wait for a few clock impulses and watch the output values
of the register, which should appear more or less random.
Depending on the logic used in the feedback path, the register
follows a predefined sequence of states, with a maximum sequence
length of (2^n)-1 in a n-bit register.
Perhaps the most important use of LFSRs is as pseudorandom number
generators, especially for automatic selftest, because the
generators are very cheap and can be run at very high clock frequencies.
With a register of n+1 bits, each n-bit input value can be generated.
Naturally, subsequent output values are highly correlated, as
only the first bit changes while all other bits are simply shifted.
Note that the feedback logic used in many textbooks has the stable
state 0000..00, while all other states are in the single large
pseudorandom sequence of the primitive polynom corresponding to the
feedback path.
Unfortunately, this means that a default realization with a
power-on initialization to the all-zero state will not work,
because the register would stay forever in the all-zero state.
One obvious workaround is to use a power-on initialization to some
other state, e.g. all-ones via flipflops with set inputs.
The other possibility, used in this applet, is to change the feedback
path so that the all-zero state is not stable.
Run the applet | Run the editor (via Webstart)
DescriptionA simple 8-bit linear feedback shift register
built from D-flipflops.
In this example, the outputs of flipflops 8,6,5,4 are summed
via XNOR gates (this is a linear operation, hence the name)
and fed back into the first flipflop.
Just wait for a few clock impulses and watch the output values
of the register, which should appear more or less random.
Depending on the logic used in the feedback path, the register
follows a predefined sequence of states, with a maximum sequence
length of (2^n)-1 in a n-bit register.
Perhaps the most important use of LFSRs is as pseudorandom number
generators, especially for automatic selftest, because the
generators are very cheap and can be run at very high clock frequencies.
With a register of n+1 bits, each n-bit input value can be generated.
Naturally, subsequent output values are highly correlated, as
only the first bit changes while all other bits are simply shifted.
Note that the feedback logic used in many textbooks has the stable
state 0000..00, while all other states are in the single large
pseudorandom sequence of the primitive polynom corresponding to the
feedback path.
Unfortunately, this means that a default realization with a
power-on initialization to the all-zero state will not work,
because the register would stay forever in the all-zero state.
One obvious workaround is to use a power-on initialization to some
other state, e.g. all-ones via flipflops with set inputs.
The other possibility, used in this applet, is to change the feedback
path so that the all-zero state is not stable.
Run the applet | Run the editor (via Webstart)
Impressum | 24.11.06
http://tams.informatik.uni-hamburg.de/applets/hades/webdemos/35-selftest/30-lfsr/lfsr-8654_print.html
 DescriptionA simple 8-bit linear feedback shift register
built from D-flipflops.
In this example, the outputs of flipflops 8,6,5,4 are summed
via XNOR gates (this is a linear operation, hence the name)
and fed back into the first flipflop.
Just wait for a few clock impulses and watch the output values
of the register, which should appear more or less random.
Depending on the logic used in the feedback path, the register
follows a predefined sequence of states, with a maximum sequence
length of (2^n)-1 in a n-bit register.
Perhaps the most important use of LFSRs is as pseudorandom number
generators, especially for automatic selftest, because the
generators are very cheap and can be run at very high clock frequencies.
With a register of n+1 bits, each n-bit input value can be generated.
Naturally, subsequent output values are highly correlated, as
only the first bit changes while all other bits are simply shifted.
Note that the feedback logic used in many textbooks has the stable
state 0000..00, while all other states are in the single large
pseudorandom sequence of the primitive polynom corresponding to the
feedback path.
Unfortunately, this means that a default realization with a
power-on initialization to the all-zero state will not work,
because the register would stay forever in the all-zero state.
One obvious workaround is to use a power-on initialization to some
other state, e.g. all-ones via flipflops with set inputs.
The other possibility, used in this applet, is to change the feedback
path so that the all-zero state is not stable.
Run the applet | Run the editor (via Webstart)
DescriptionA simple 8-bit linear feedback shift register
built from D-flipflops.
In this example, the outputs of flipflops 8,6,5,4 are summed
via XNOR gates (this is a linear operation, hence the name)
and fed back into the first flipflop.
Just wait for a few clock impulses and watch the output values
of the register, which should appear more or less random.
Depending on the logic used in the feedback path, the register
follows a predefined sequence of states, with a maximum sequence
length of (2^n)-1 in a n-bit register.
Perhaps the most important use of LFSRs is as pseudorandom number
generators, especially for automatic selftest, because the
generators are very cheap and can be run at very high clock frequencies.
With a register of n+1 bits, each n-bit input value can be generated.
Naturally, subsequent output values are highly correlated, as
only the first bit changes while all other bits are simply shifted.
Note that the feedback logic used in many textbooks has the stable
state 0000..00, while all other states are in the single large
pseudorandom sequence of the primitive polynom corresponding to the
feedback path.
Unfortunately, this means that a default realization with a
power-on initialization to the all-zero state will not work,
because the register would stay forever in the all-zero state.
One obvious workaround is to use a power-on initialization to some
other state, e.g. all-ones via flipflops with set inputs.
The other possibility, used in this applet, is to change the feedback
path so that the all-zero state is not stable.
Run the applet | Run the editor (via Webstart)