Carry-select adder (8 bit)

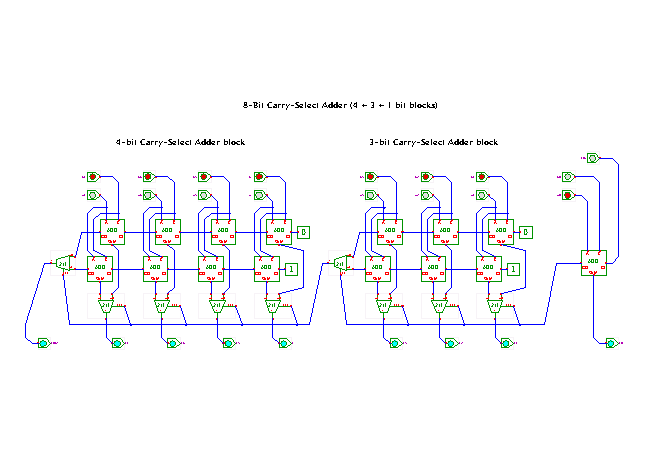Description

An 8-bit carry-select adder, built as a cascade from a 1-bit full-adder, a 3-bit carry-select block, and a 4-bit carry-select adder. Click the input switches or type the 'a', 'b', 'c' bindkeys to control the first-stage adder.

The problem of the ripple-carry adder is that each adder has to wait for the arrival of its carry-input signal before the actual addition can start. The basic idea of the carry-select adder is to use blocks of two ripple-carry adders, one of which is fed with a constant 0 carry-in while the other is fed with a constant 1 carry-in. Therefore, both blocks can calculate in parallel. When the actual carry-in signal for the block arrives, multiplexers are used to select the correct one of both precalculated partial sums. Also, the resulting carry-out is selected and propagated to the next carry-select block.

In total, the carry propagation time through an n-bit adder block is reduced from O(n) to the number of stages times the delay of the multiplexers. Naturally, using n blocks of 1-bit carry-select adders would incur a complexity of n multiplexers, again resulting in O(n) delay. Therefore, a partition with (slowly) increasing block-size is chosen. In the example, the first (least-significant) block consists of a simple full adder, followed by a 3-bit carry-select block, and finally a 4-bit carry-select block. A common choice for a 16-bit carry-select adder is to use a 6-4-3-2-1 bit partitioning. While the delay of the standard ripple-carry adder with n-bits is O(n), the delay through the carry-select adder behaves as O(sqrt(n)) at a hardware cost of O(3*n).

To demonstrate this behaviour, a very large gate-delay is used for the gates inside the 1-bit adders - resulting in an addition time of about 0.6 seconds per adder. The total carry-propagation time is therefore 0.6 seconds for the first adder, and another 1.2 seconds through both carry-select blocks, for a total of 1.8 seconds from the (A0,B0,Cin) inputs to the (Cout) output. The longest delay path is this circuit is through the four-bit ripple-carry block from (A4,B4) to (Cout), for a total delay of 2.4 seconds. Even in this (small) example, the carry-select adder is much faster than the ripple-carry adder at 4.8 seconds.

Run the applet | Run the editor (via Webstart)