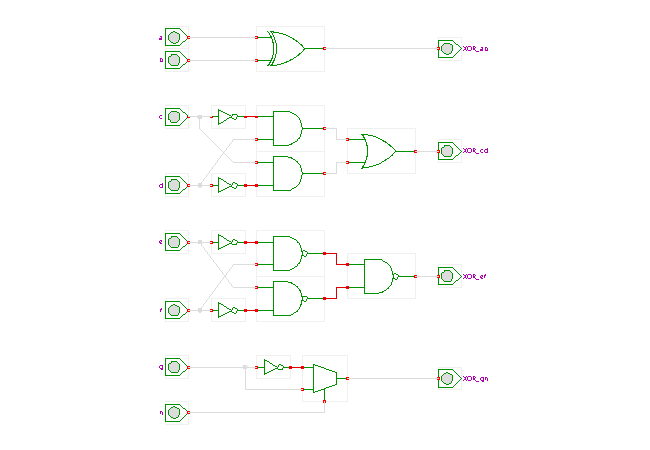| |
DescriptionThis applet shows four different realizations of a two-input XOR gate.
It is meant to highlight the point that (indefinitely) many different
but logically equivalent realizations exist for every logic function.
Which of the different variants is best depends on technological
constraints like the size, speed, and power-consumption of the available
basic and complex gates.
Click the input switches, or type the 'a', 'b', 'c', ... 'h' bindkeys to control the different XOR gates.
The topmost circuit uses a single XOR-gate. While this seems the simplest realization, the basic XOR gate cannot be realized directly as a basic gate in standard VLSI technologies.
The second circuit shows the standard expansion of the XOR function
XOR(c,d) = (c & !d) | (!c & d).In the third circuit, de'Morgan rules have been used to rewrite the above expansion with NAND-gates instead of the AND-gates and OR-gate. Again, as demonstrated in the twelve-input AND-gate applet, the NAND-based realization is cheaper and faster in most current VLSI technologies.
The fourth circuit shows how to realize the XOR function with a multiplexer and an inverter. This might seem a little odd at first, but multiplexers turn out to be very flexible building blocks. Many logic functions can be realized with surprisingly low number of multiplexers, based on clever assignments of the data and control inputs. This fact is used in a famous family of programmable logic devices, where multiplexers are used as the basic blocks to implement all logic functions including flipflops. For a live demonstration, visit the ACT1 demonstration applet pages. In this case, the higher cost of the multiplexers (as compared to basic gates) is more than outweighed by the great flexibility and the reduced number of external wires. Special logic synthesis algorithms have been developed to make efficient use of multiplexer-based structures.
Run the applet | Run the editor (via Webstart)